


| données | vraisemblance | séparation |
|---|---|---|

|

|

|
| données | vraisemblance | EM |
|---|---|---|

|

|

|
| données | EM |
|---|---|

|

|

|

|
| 0.2 | 1 | 20 |
|---|---|---|

|

|

|
| 0.5 | 0.99 | 1.1 |
|---|---|---|

|

|

|
| 2 | 4 | 8 |
|---|---|---|

|

|

|

|

|
| bruité | débruité |
|---|---|

|

|

|

|

|

|
| bruité | débruitage |
|---|---|

|

|

|

|

|

|
| bruité | débruitage |
|---|---|

|

|

|

|

|

|
| original | buité | débruité |
|---|---|---|

|

|

|
| Image cible | Image source | Résultat |
|---|---|---|

|

|

|
| Image cible | Image source | Résultat |
|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|
Isolation des lignes horizontales

|
Isolation des lignes verticales

|
Isolation des lignes diagonales

|
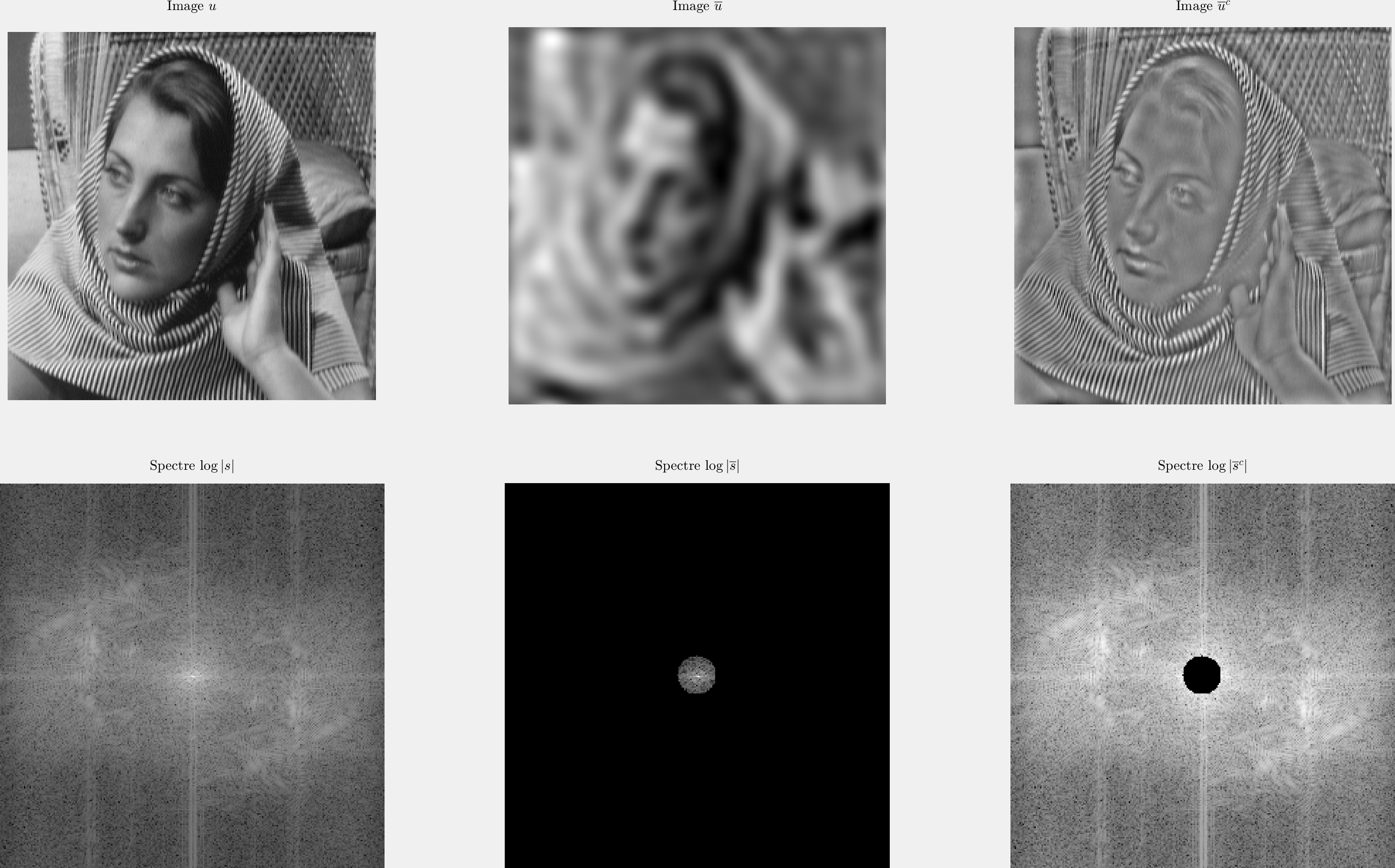
|

|

|

|

|

|

|

|

|

|
| Image originale | Sinogramme | Image reconstituée |
|---|---|---|

|

|

|

|

|

|

|

|
| Audio | Spectrogramme |
|---|---|
|
|

|
|
|

|
|
|

|
|
|

|
| Audio | Spectrogramme |
|---|---|
|
|

|
|
|
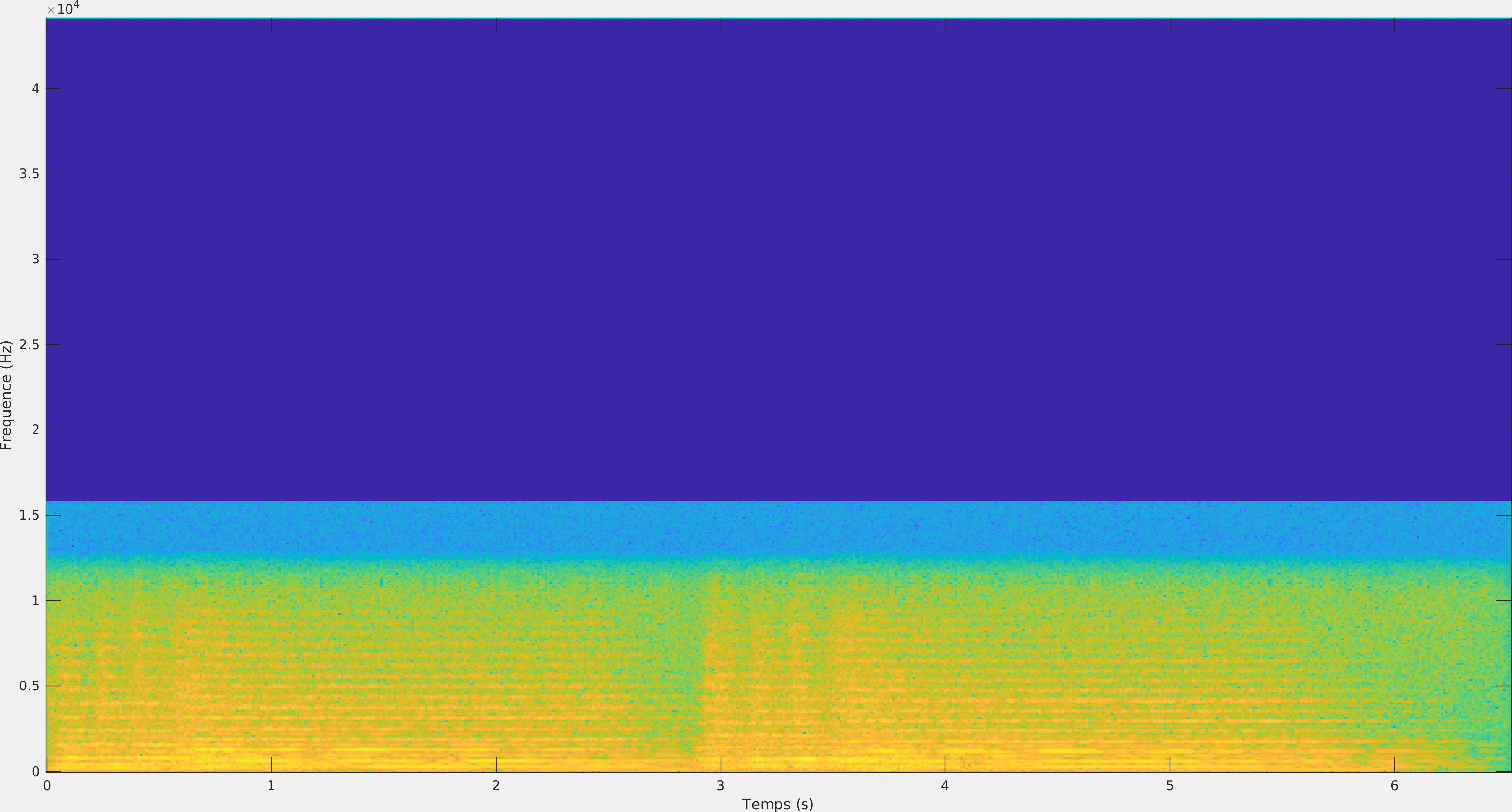
|
|
|

|
|
|
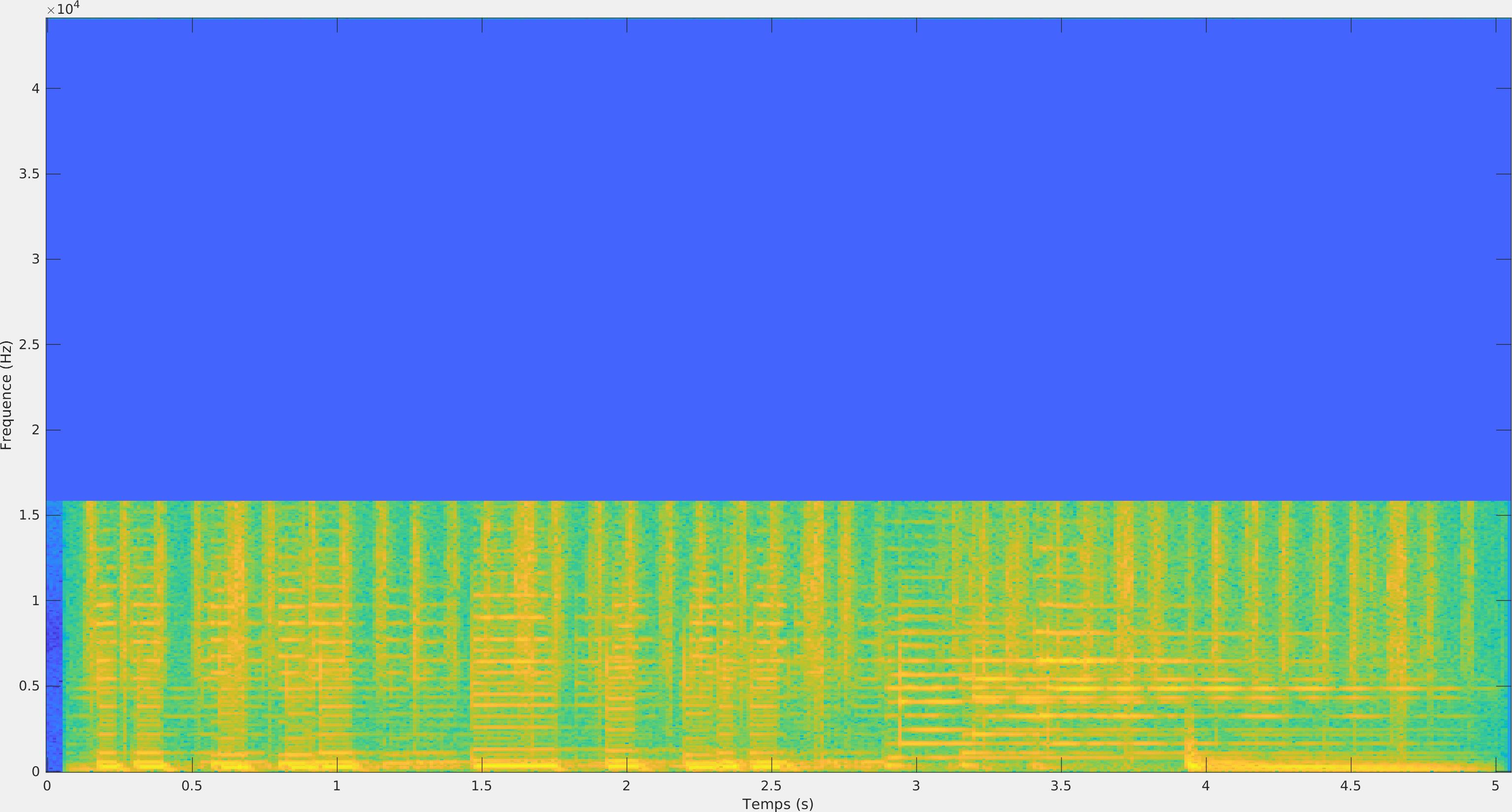
|
| Audio | Spectrogramme |
|---|---|
|
|

|
|
|

|
|
|

|
|
|

|
| Audio bruité | Audio débruité |
|---|---|

|

|
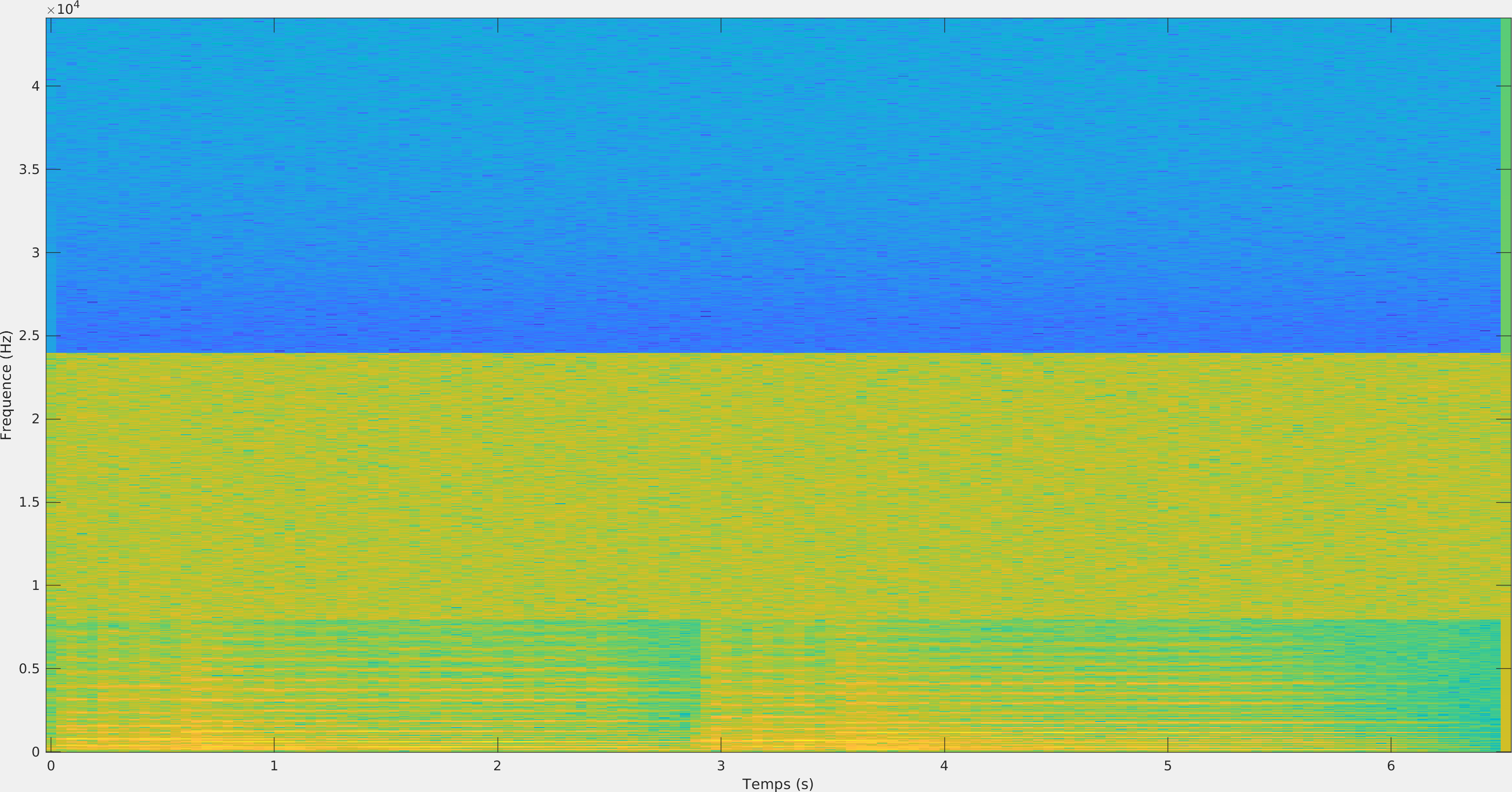
|

|

|
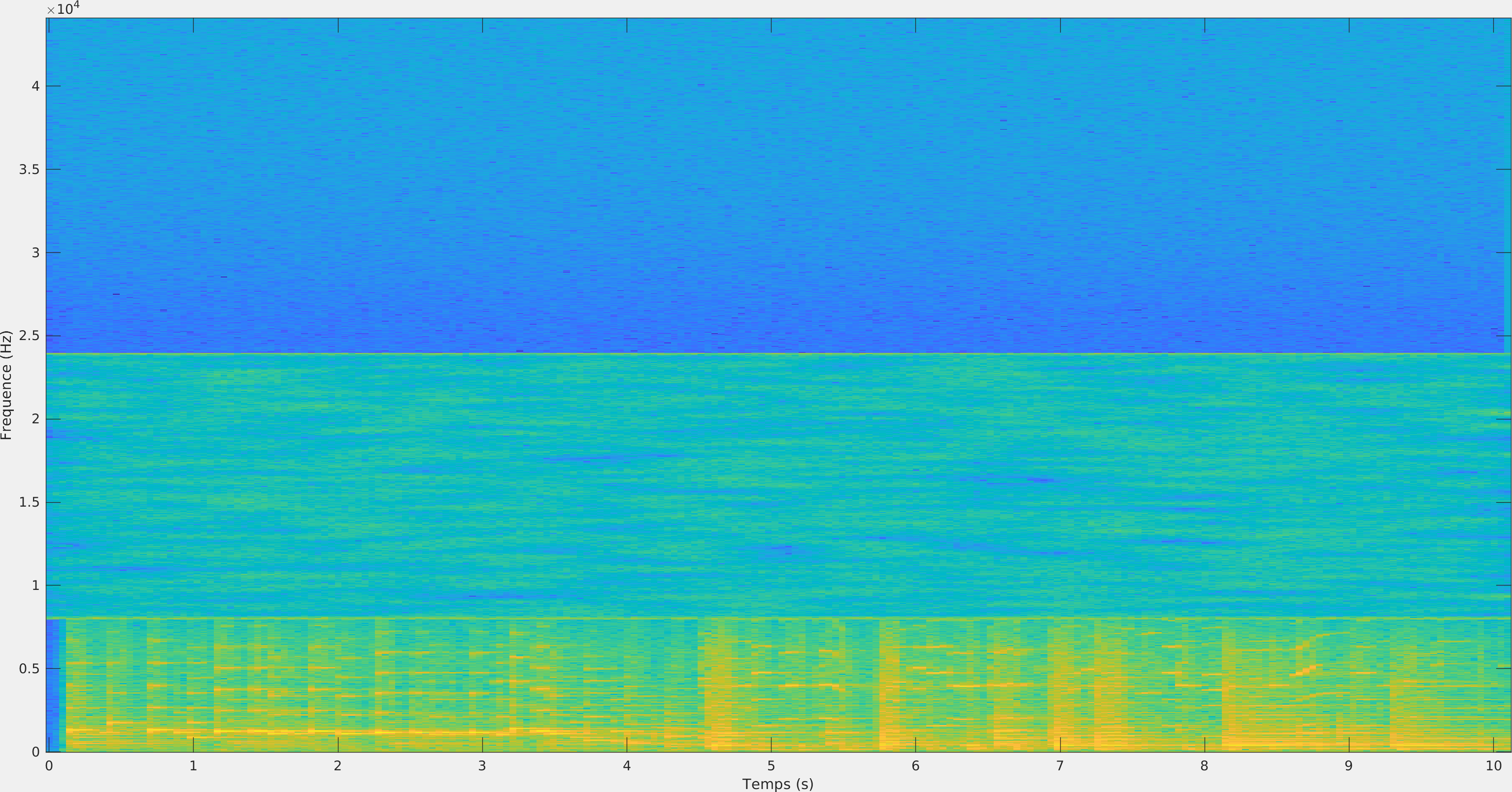
|

|

|

|

|

|

|

|

|

|

|
| Harmoniques (violon) | Percussions (batterie) |
|---|---|

|

|
| Audio | Spectrogramme |
|---|---|
|
|
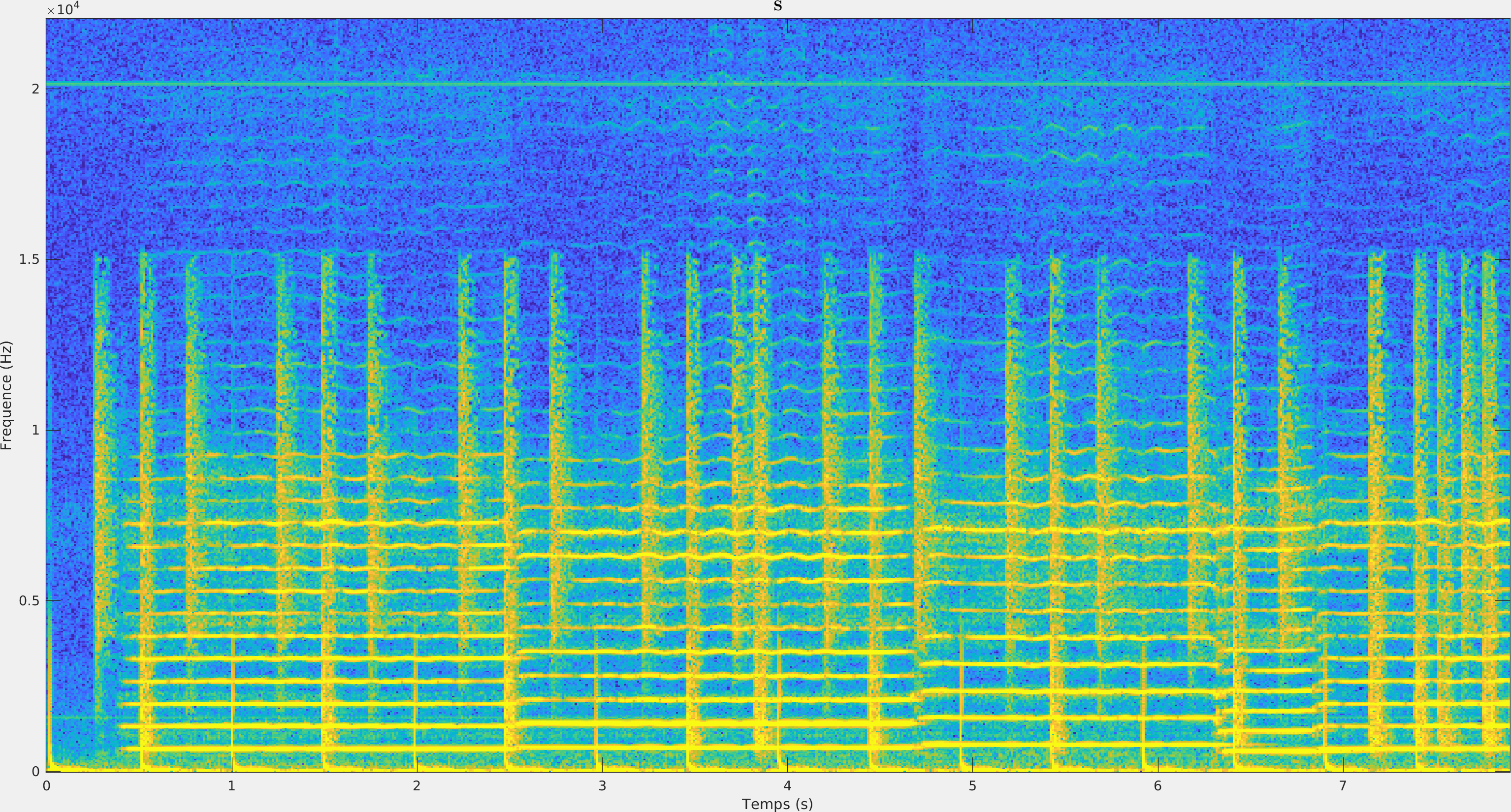
|
| Masque harmoniques | Masque percussions |
|---|---|

|

|
| Harmoniques | Percussions |
|---|---|

|

|

|

|
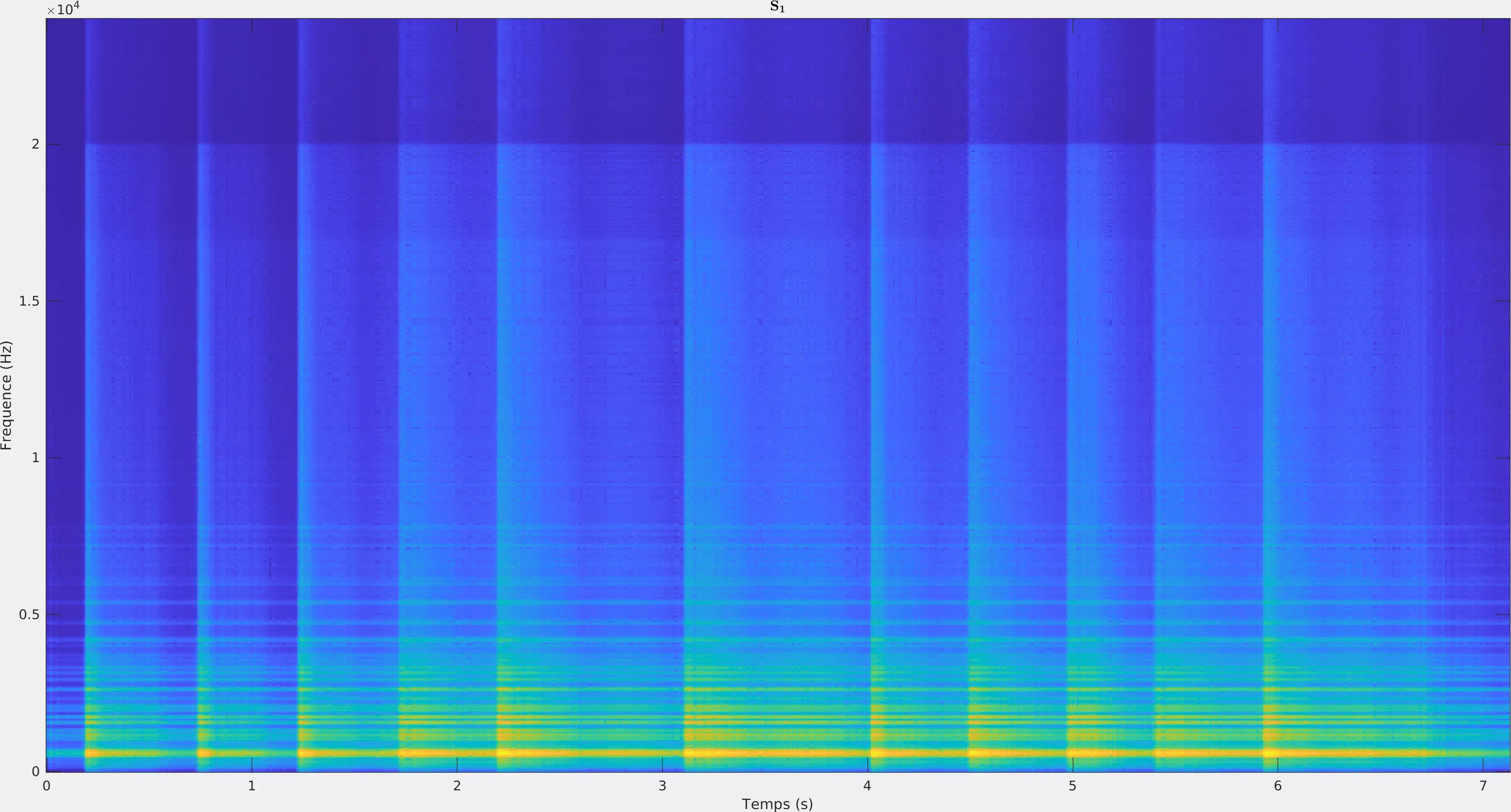
|
| Audio | Spectrogramme |
|---|---|
|
|

|
|
|

|
|
|

|
|
|

|

|

|

|

|

|

|

|

|

|
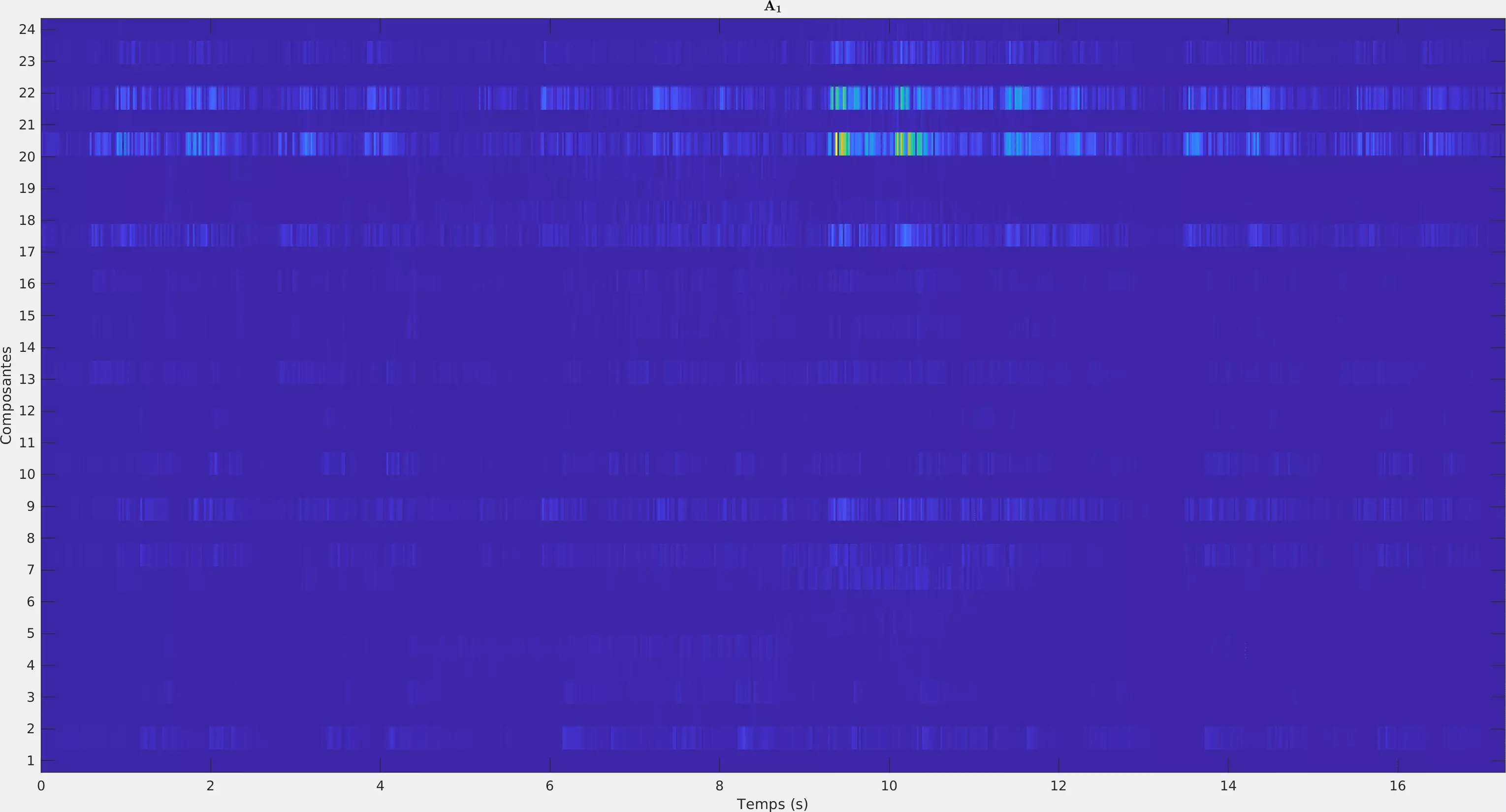
|

|

|