projet-probleme-inverse-3D/docs/slides.md

theme	class	coverAuthor	coverBackgroundUrl	coverBackgroundSource	coverBackgroundSourceUrl	coverDate	themeConfig	title
academic	text-white	Laurent Fainsin, Damien Guillotin, Pierre-Eliot Jourdan	https://images.unsplash.com/photo-1655720408861-8b04c0724fd9?ixlib=rb-4.0.3&ixid=MnwxMjA3fDB8MHxwaG90by1wYWdlfHx8fGVufDB8fHx8	unplash	https://unsplash.com/photos/Vc0CmuIfMg0	2023-02-01	paginationX paginationY paginationPagesDisabled r t 1	Bureau d'étude de PI3D

Bureau d'étude de PI3D

Sujet 6 - Reformulation du MVS par level sets

---

Plan du BE

• Définitions
• L'idée générale
• Hyposthèses
• L'algorithme
• Résultats
• Conclusion

---

Définition

Level sets

\mathcal{V} = \{ \textbf{Q} = (X, Y) \in \mathbb{R}^2, u(\textbf{Q}) > s \}, \quad s\in [0,1], \quad u \colon \mathbb{R}^2 \to [0, 1]

---

Exemple Level sets 3D

Marching cubes

---

Définition

Multi-view Stereo

Concurrent Stereo Reconstruction, Martin R. Oswald, 2007

---

L'idée générale

Évolution de u

Variational principles, surface evolution, PDEs, level set methods, and the stereo problem - Olivier Faugeras, Renaud Keriven, 1998

---

L'idée générale

Évolution de u

Variational principles, surface evolution, PDEs, level set methods, and the stereo problem - Olivier Faugeras, Renaud Keriven, 1998

---

Hypothèses

Discrétisation de l'espace

\mathbb{R}^3 \to \mathbb{V}

Binarisation du levelset

\mathcal{V} = \{ \textbf{v} = (x, y, z) \in \mathbb{V}, u(\textbf{v}) > 0 \}, \quad u \colon \mathbb{V} \to \{0, 1\}

Wikipedia

---

L'algorithme

Initialisation du volume

• Définition des bornes de notre grille de voxels:
  • x \in \llbracket x_{\min}, x_{\max} \rrbracket
  • y \in \llbracket y_{\min}, y_{\max} \rrbracket
  • z \in \llbracket z_{\min}, z_{\max} \rrbracket
• Définition d'une résolution de voxel:
  • Pas trop grand, sinon un voxel projeté sur nos caméras comprends plusieurs pixels
  • Pas trop petit, sinon plusieurs voxels se projetent sur le même pixel
  • Exemple: 5.10^{-2}\ m
• Initialisation des valeurs des voxels:
  • Uniforme: \forall \textbf{Q} = (X, Y, Z) \in \mathbb{R}, u_0(\textbf{Q}) = 1
  • Shape From Silhouette BE4 CHEH

---

L'algorithme

Principe du Shape from Silhouette

Implementation of a Shadow Carving System for Shape Capture, doi: 10.1109/TDPVT.2002.1024034

---

Shape from Silhouette 3D

---

L'algorithme

Lancer de rayon (Fast Voxel Intersect)

---

Résultats

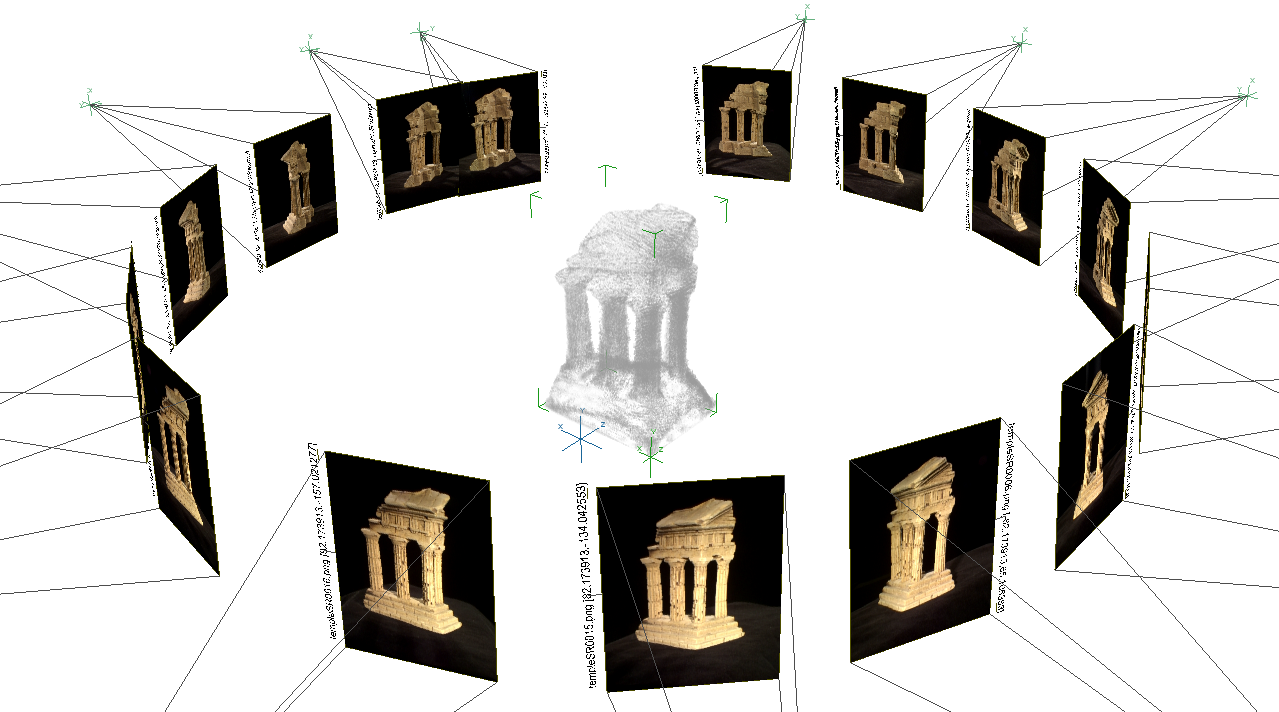
L'environnement

---

Résultats

Les données

---

Résultats

L'initialisation (Shape from Silhouette)

---

Résultats

Bordures

---

Résultats

Visibilité des voxels

---

Résultats

Évolution du level set

---

Conclusion

Ce que nous avons fait

• Réalisation du SfS en 2D/3D
• Réalisation du MVS par level sets en 2D avec initialisation par SfS

Axes d'amélioration soon™

• Résultat en 3D
• \{0, 1\} \to [0, 1]