projet-long/slides.md

theme	class	coverBackgroundUrl	coverBackgroundSource	coverBackgroundSourceUrl	coverDate	themeConfig	title
academic	text-white	https://plus.unsplash.com/premium_photo-1673553304257-018c85e606f8?ixlib=rb-4.0.3&ixid=MnwxMjA3fDB8MHxwaG90by1wYWdlfHx8fGVufDB8fHx8	unplash	https://unsplash.com/photos/g4I556WCJT0		paginationX paginationY paginationPagesDisabled r t 1	Projet Long

Sphere detection and multimedia applications

2023-03-09 Laurent Fainsin, Pierre-Eliot Jourdan, Raphaëlle Monville-Letu, Jade Neav

---

Contents

• Types of spheres
• Automatic sphere detection
• Lighting intensity estimation
• Lighting direction estimation

Architecture

Cinema

3D Reconstruction

pexels

---

class: text-white custombg

Types of spheres

---

class: text-white custombg2

Chrome sphere

CaveAcademy

---

Acquisition techniques

Louis du Mont

---

Realistic lighting

High Dynamic Range Imaging, Paul Debevec

---

class: text-white custombg3

Shiny sphere

CaveAcademy

---

class: text-white custombg4

Matte sphere

CaveAcademy

---

Automatic sphere detection

• Model
• Datasets
• Results
• Perspectives

---

Model

End-to-End Object Detection with Transformers, arXiv:2005.12872

---

Datasets (1/4)

Antoine Laurent

---

Datasets (2/4)

A Dataset of Multi-Illumination Images in the Wild

---

Datasets (3/4)

MS COCO compositing

---

Datasets (4/4)

Blender, PolyHaven

---

Results (1/8)

---

Results (2/8)

---

Results (3/8)

---

Results (4/8)

---

Results (5/8)

---

Results (6/8)

---

Results (7/8)

---

Results (8/8)

---

Perspectives

Poliigon.com

---

Lighting intensity estimation

• Photometric Stereo
• Lambert Law
• Problem formulation
• Algorithms
• Generated images
• Results
• Perspectives

---

Photometric Stereo

• Estimate the surface normals of an object
• Shiny spheres \rightarrow direction of the lighting

Wikipedia

---

Lambert law

I(q) = \rho(Q) \times \vec{n}(Q) \cdot \vec{s}(Q)

• \rho(Q) is the albedo

• \vec{n}(Q) is the normal vector

• \vec{s}(Q) = \phi \times \vec{s_0}(Q) is the lighting direction

LaserFocusWorld

---

Problem formulation

N lightings, P pixels
\rightarrow I = M \times S \times D_{\phi}

• I \in \mathbb{R}^{P \times N} \rightarrow gray scale levels \rightarrow known from image pixels

• M \in \mathbb{R}^{P \times 3} \rightarrow the albedo and the normals \rightarrow unknown

• S \in \mathbb{R}^{3 \times N} \rightarrow direction of lightings \rightarrow known from shiny spheres

• D_{phi} = diag(\phi_1,...,\phi_{N}) \in \mathbb{R}^{ N \times N} \rightarrow intensities of lightings \rightarrow to be determined

---

Algorithm 1

Intensities : [\phi_1,...,\phi_{N}]

New values : \phi_j \plusmn \delta, \ j \in [1,..,N]

Estimation of the matrix M

Mean-squared error : \underset{\phi_i}{\min} || I - M S D_{\phi} ||_2^2

Update the value of \phi_j

Repeat previous steps

---

Algorithm 2

Algorithm 1 \rightarrow too long

I = M S D_{\phi} \iff M = I(S D_{\phi})^\dagger = I (S D_{\phi})^T [(S D_{\phi})(S D_{\phi})^T]^{-1}

Lambert law :

$$ \begin{align*} I &= I (S D_{\phi})^T [(S D_{\phi})(S D_{\phi})^T]^{-1} S D_{\phi} \ &= I D_{\phi} S^T S^{-T} D_{\phi}^{-2} S^{-1} S D_{\phi} \end{align*}

New residual :

\underset{\phi_i}{\min} || I - I D_{\phi} S^T S^{-T} D_{\phi}^{-2} S^{-1} S D_{\phi} ||_2^2

---

Generated images

---

Results (1/2)

---

Results (2/2)

---

Real images

---

Results

---

Perspectives

3D reconstruction

---

Lighting direction estimation

• Estimation of lighting vector
• Neural Network
• Real data
• Generated data
• Results
• Perspectives

---

Estimation of lighting vector

flowchart LR
  id1[Bounding box of the sphere]
  id2[Deduce the normals]
  id3[Resolution of I = s * n]

  id1 --> id2
  id2 --> id3

---

Neural Network

---

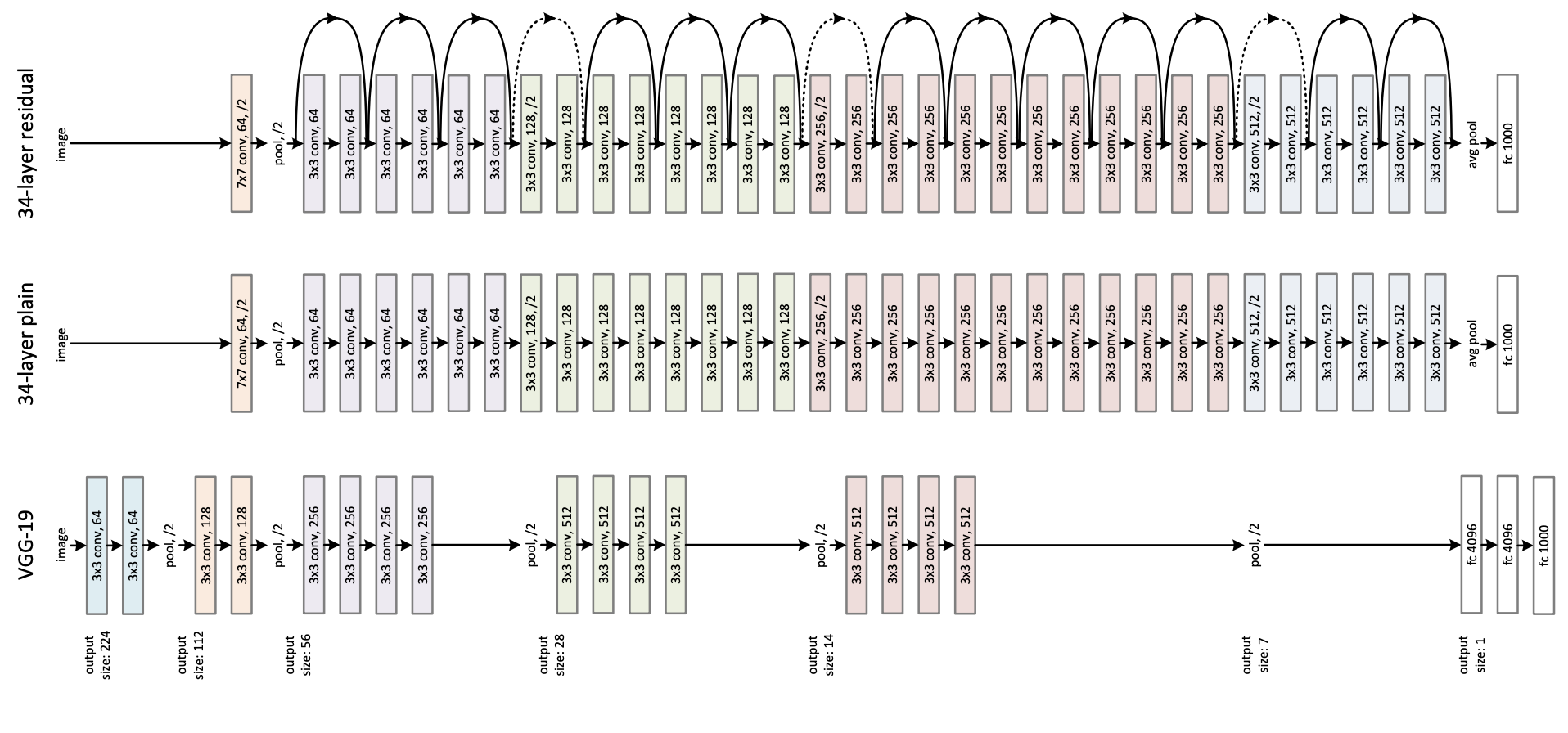
ResNet-50

---

Real data : creation of mask

---

Generated data with blender

Simulated matte spheres
Generated data with different lightings

---

Results

---

Perspectives

• Create more data to prevent overfitting
• Diversify the types of data lighting (more than 8 directions)
• Transform the model into something more general:
  \rightarrow from {image of sphere, vector lighting} to {image of objects, vector lighting}